

ASTRO ELECTRONIC
Dipl.-Ing. Michael Koch
Raabestr. 43 D-37412 Herzberg Germany
Tel: +49 (0)5521 854265 Fax: +49 (0)5521 854266www.astro-electronic.de e-mail
Von November 2005 bis April 2006 wurde ein selbstgeschliffener Spiegel auf die Reise geschickt, damit er von möglichst vielen Spiegelschleifern getestet werden konnte. Das Ziel war die Testmethoden und Ergebnisse vergleichen zu können. Die Aktion wurde von Martin Trittelvitz organisiert, und der Spiegel wurde von Chris Plicht zur Verfügung gestellt.
Die sachliche Diskussion über dieses Test-Protokoll ist ausdrücklich erwünscht. Es gehört für mich zum guten Umgangston dass diese Diskussion nur in solchen Foren stattfinden sollte, in denen ich auch regelmässig mitlese, also konkret im Astro-Treff/ATM-Optik-Forum: http://www.astrotreff.de/forum.asp?FORUM_ID=37 Ich werde mich nicht an Diskussionen beteiligen, die in irgendwelchen anderen Foren geführt werden.
COPYRIGHT:
Dieses Test-Protokoll ist urheberrechtlich geschützt. Die Vervielfältigung,
egal ob ganz oder teilweise, ist nur mit ausdrücklicher schriftlicher
Genehmigung des Autors zulässig. Das gilt auch für Zitate. Wer
auf dieses Test-Protokoll verweisen möchte, der möge bitte einen
Link verwenden.
1.
Foucault-Test
 |
 |
Der Foucault-Tester entspricht ziemlich genau der Bauanleitung in Texereau's "How to make a Telesope", also feststehende Lichtquelle mit vertikaler Schlitzmaske, weisses Halogen-Licht. Der einzige Unterschied ist dass direkt vor dem Schlitz ein unter 45° angeordneter Planspiegel sitzt, um den seitlichen Abstand zwischen Lichtquelle und Messerschneide zu minimieren. Die Auswertung erfolgt mit einem selbstgeschriebenen Programm, in enger Anlehnung an den Algorithmus wie er bei Texereau beschrieben ist. Als Licht-Wellenlänge habe ich 633nm eingetragen, um die Ergebnisse besser mit der interferometrischen Auswertung vergleichen zu können. Ich verwende eine Couder-Maske mit 9 Zonen.
Erste Messreihe, die "1|4" Markierung ist oben:
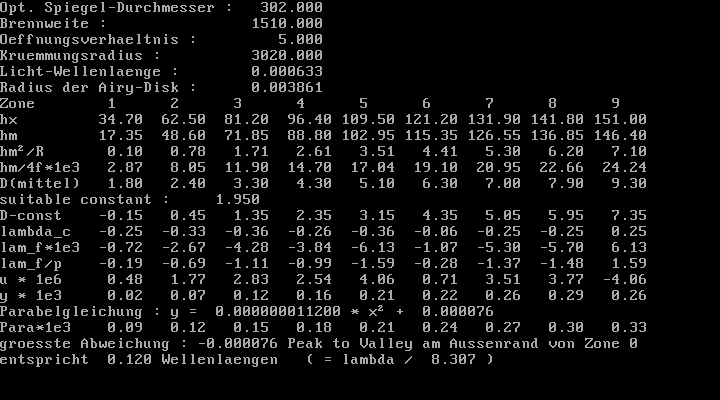
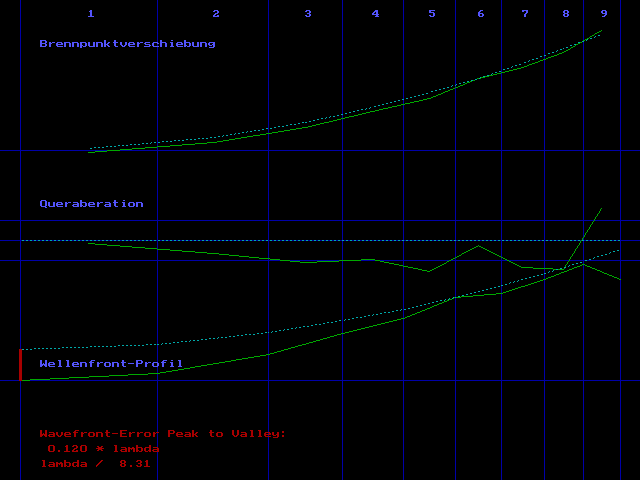
Zweite Messreihe, Spiegel um 90° im Uhrzeigersinn gedreht, die "3" Markierung ist oben:
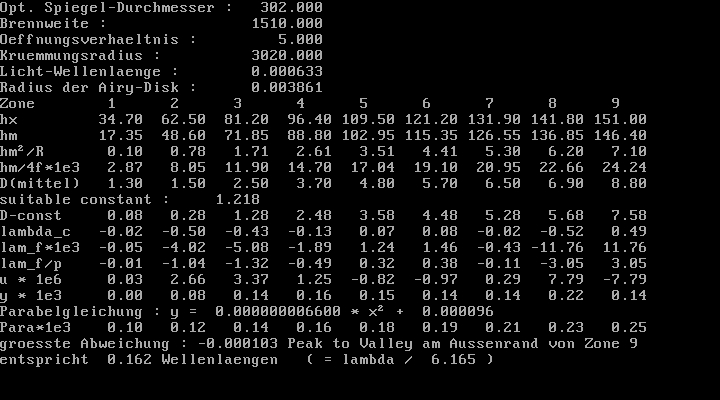
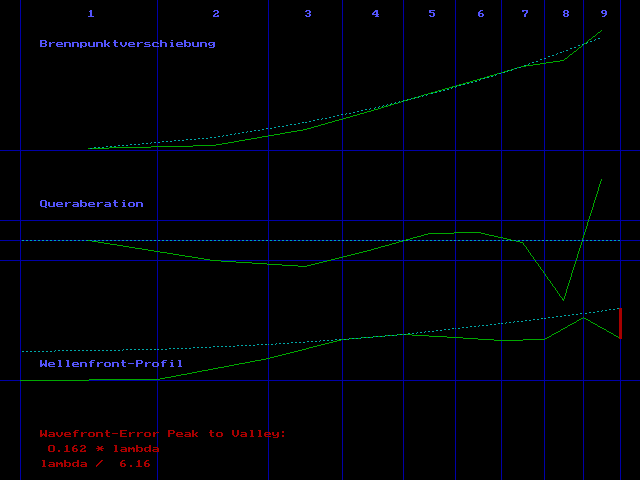
Kombinierte (gemittelte) Auswertung der beiden Messreihen:
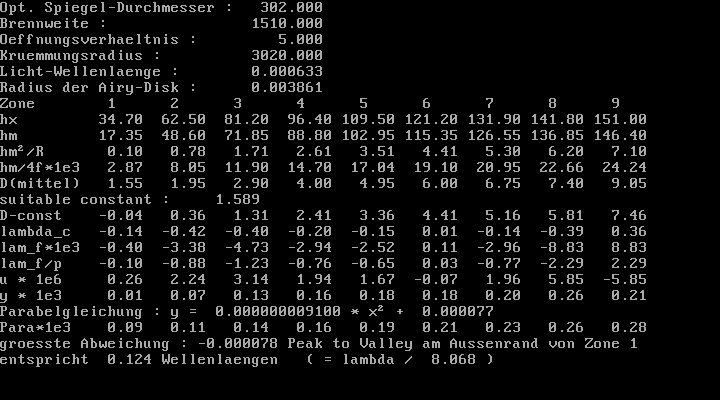
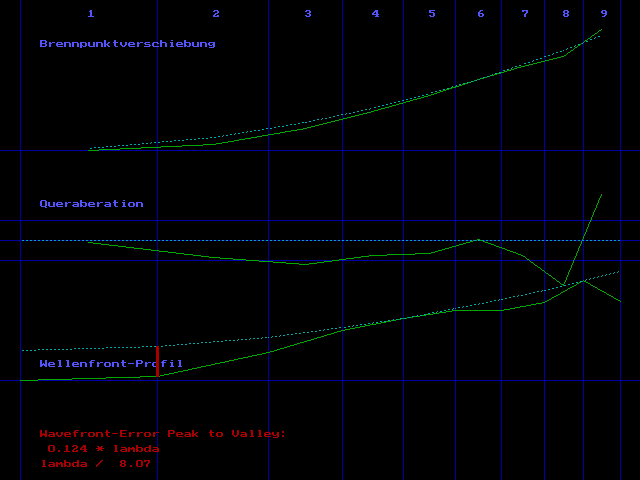
Mein
erster Eindruck nach dem Foucault-Test: Ein guter Spiegel, insgesamt leicht
überkorrigiert.
2. Interferometrischer Test
Der
nächste Test ist ein direkter Test des Spiegels gegen die Transmissions-Sphäre
eines Fizeau-Interferometers.
Das
Interferometer ist ein modernisiertes Zygo MK-III mit Phasenschieber, die
Transmissions-Sphäre ist eine Zygo 4" f/3.3 (Series II) mit weniger
als 1/15 wave Oberflächen-Fehler. Da hier nur der mittlere f/10 Bereich
der Sphäre verwendet wird, kann man annehmen dass der Fehler deutlich
kleiner als 1/15 wave ist. Die Auswertung erfolgt über die IntelliWave
Software.

Bei
der ersten Messung war der Spiegel so ausgerichtet dass die "1|4" Markierung
oben war. Das Interferometer dreht aber das Bild um 180°, so dass die
"1|4" Markierung im Interferogramm unten ist.
Gemessen
wird die Wellenfront, d.h. die "waves/fringe" Konstante ist 1.0.
Verkippung
und Fokus wurden automatisch subtrahiert. Es wurden automatisch 10 Messungen
gemittelt.
Wie
ich leider erst hinterher gemerkt habe ist bei allen interferometrischen
Messungen das Vorzeichen falsch: Rot sind also Täler, violett sind
Berge.
Man
sieht die gleiche Wellenfront-Topografie links als 2D-Darstellung und rechts
als 3D-Darstellung. Ganz links sind die Zernike-Koeffizienten aufgelistet.
Man
sieht sofort zwei Dinge:
1.
Jede Menge sphärische Aberation, das muss so sein weil hier ein Paraboloid
gegen eine Sphäre gemessen wurde.
2.
Ziemlich viel Astigmatismus.
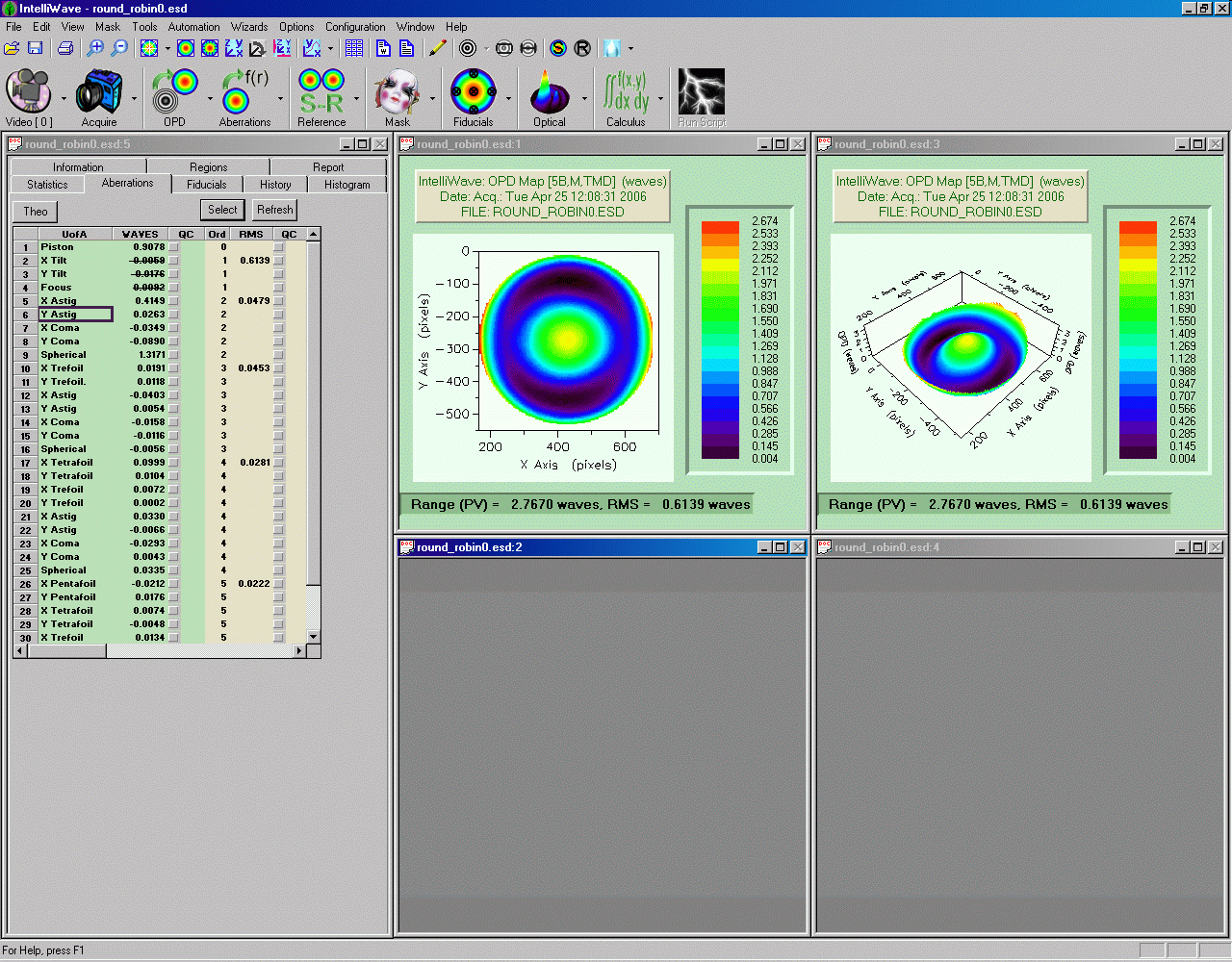
Im
nächsten Bild wurde die theoretische Differenz zwschen Paraboloid
und Sphäre subtrahiert. Im konkreten Fall sind das 1.242 waves für
den "spherical" Term. Berechnungsgrundlagen siehe http://www.astro-electronic.de/faq3.htm#6
(Link geändert am 6.8.06)
Oben
links: Die gemessenen Rohdaten
Oben
rechts: Die zu subtrahierende sphärische Aberation, 1.242 waves
Unten
links: Die Differenz als 2D-Darstellung
Unten
rechts: Die Differenz als 3D-Darstellung
Ganz
links: Die Zernike-Koeffizienten nach der Subtraktion
Man sieht dass der "spherical" Term nach der Subtraktion immer noch positiv ist, der Spiegel ist also etwas überkorrigiert.
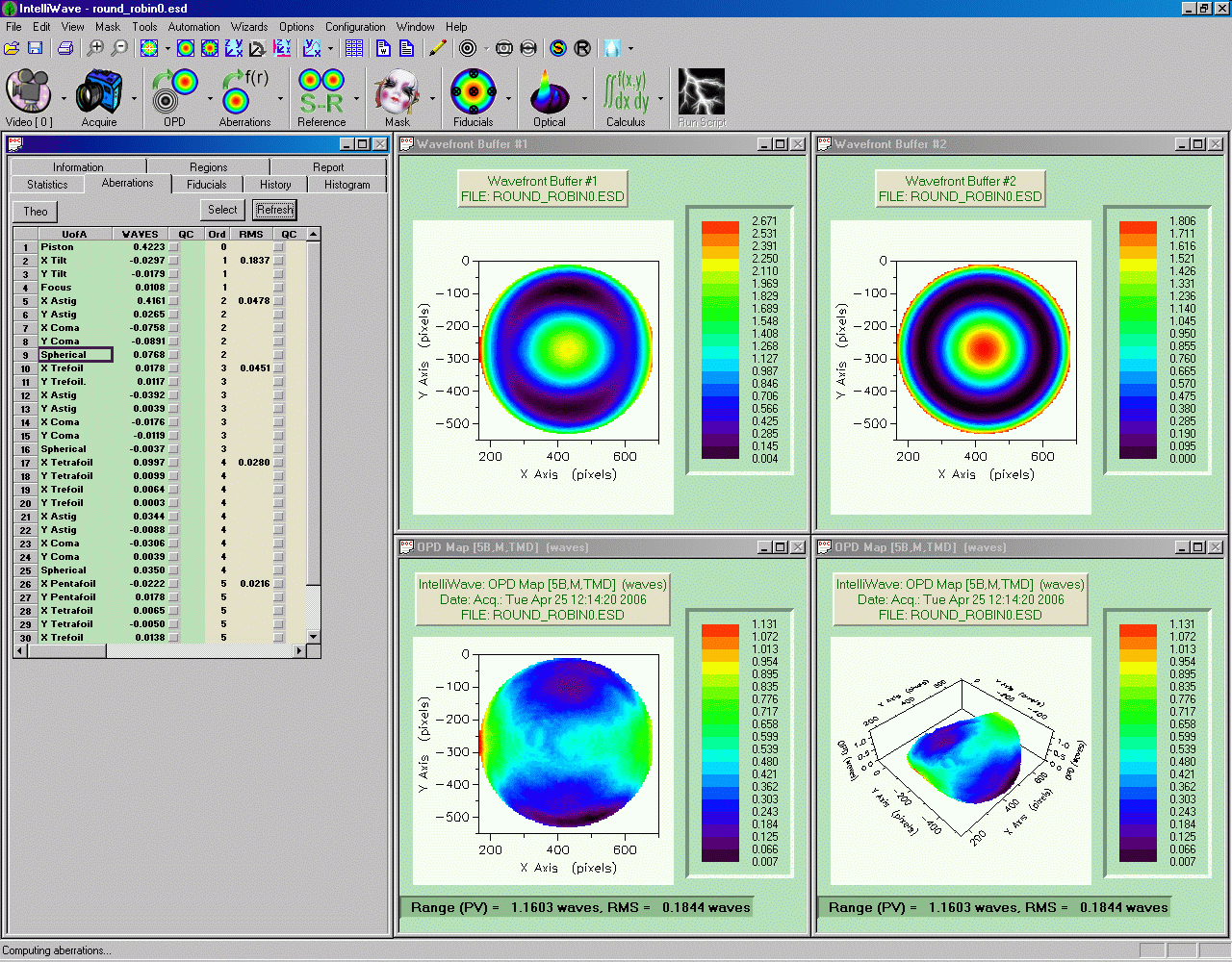
Jetzt habe ich den Spiegel um 90° im Uhrzeigersinn gedreht, so dass die "3" Markierung oben ist.
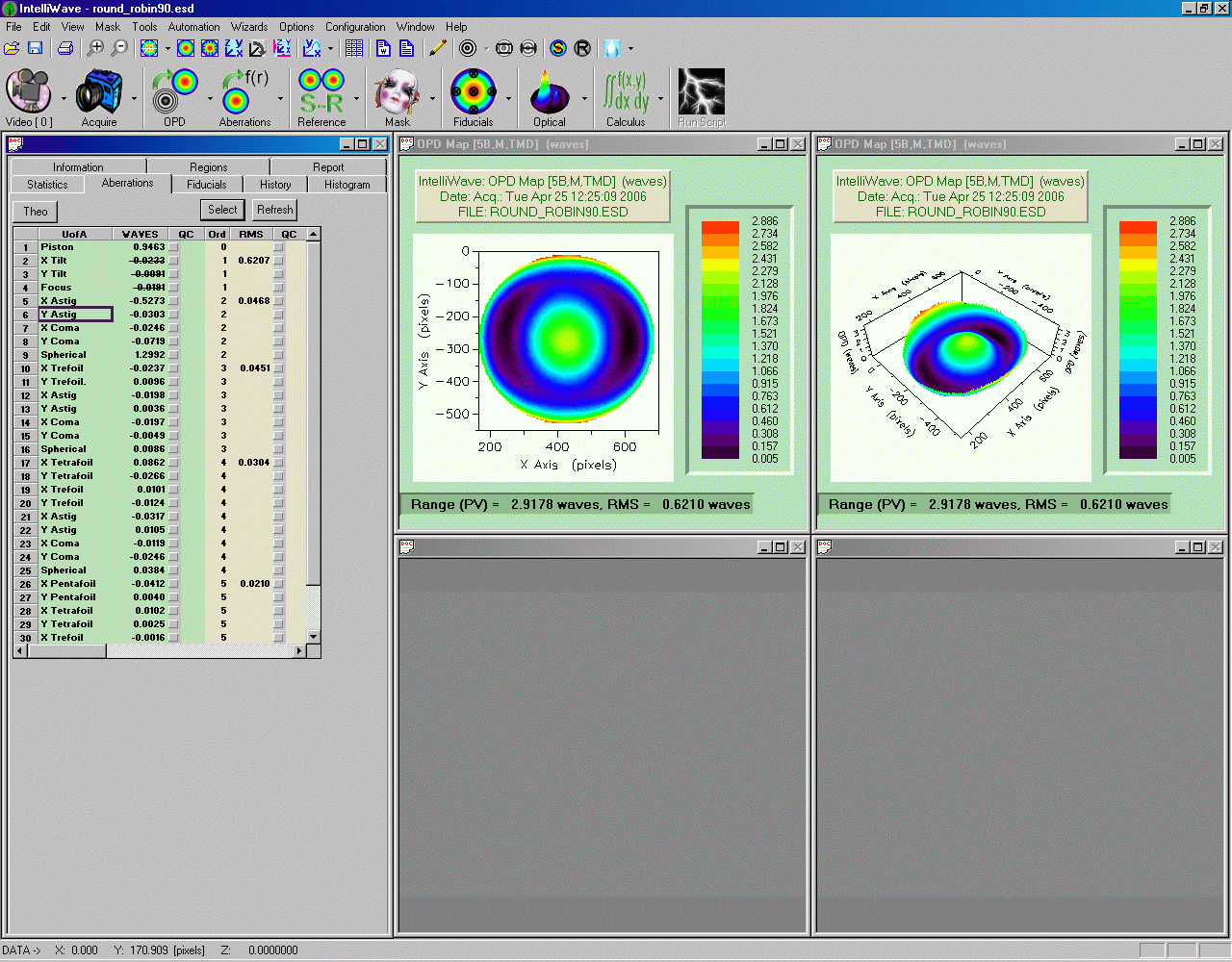
Und nach Abzug der sphärischen Aberation sieht es so aus:
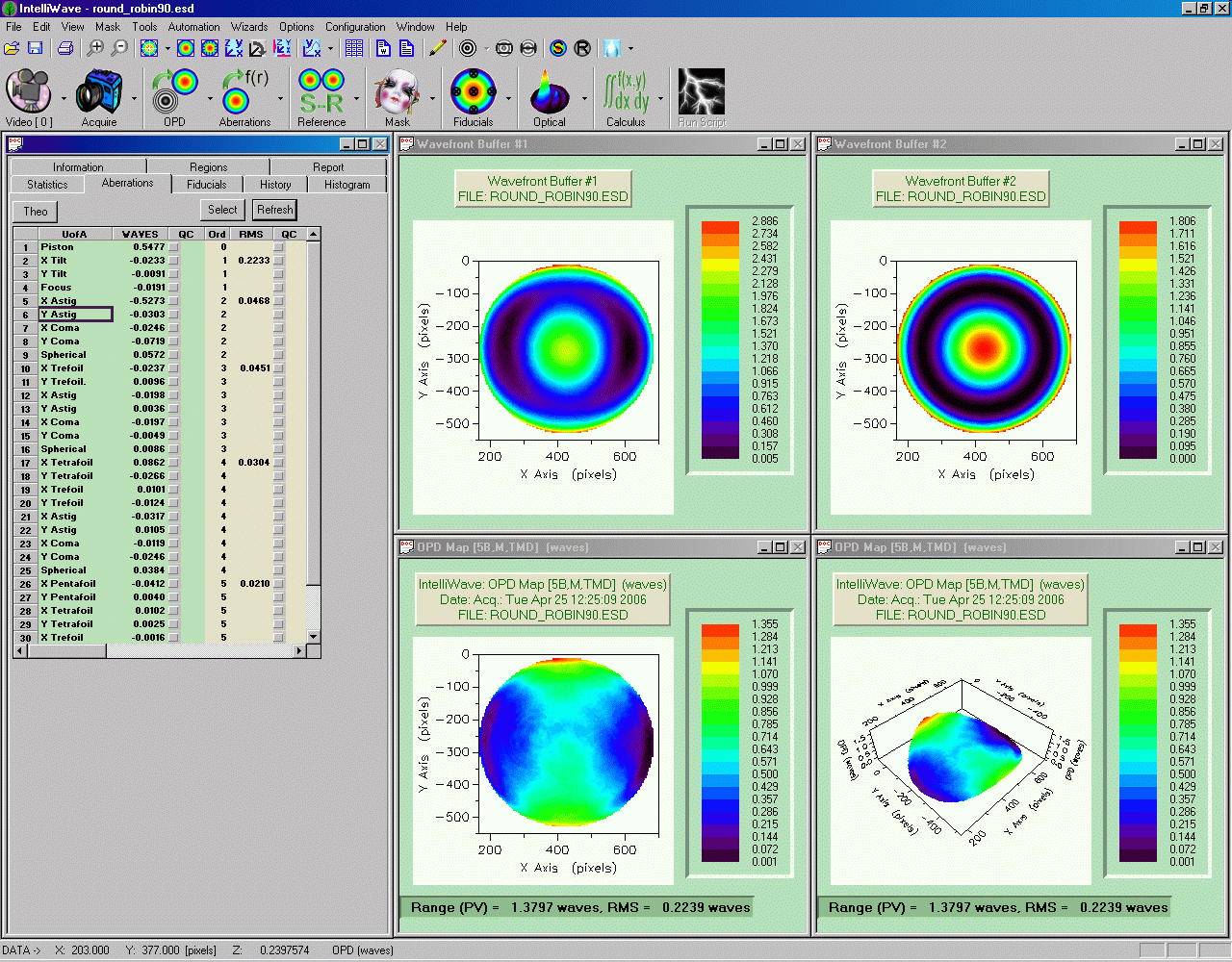
Abschätzung
des Teststand-Astigmatismus: (Herleitung siehe http://www.astro-electronic.de/faq3.htm#11,
Link geändert am 6.8.06)
z4_m0
= 0.4161
z4_m90
= -0.5273
Teststand-Astigmatismus:
(0.4161 + (-0.5273)) / 2 = -0.0556
Wahrer
X-Astigmatismus (Z4) des Spiegels: (0.4161 - (-0.5273)) / 2 = 0.4717
-->
Der Teststand-Astigmatismus ist hier vernachlässigbar gering.
Ergebnis
der interferometrischen Messung, nach Mittelung der 0° und 90°
Messungen:
Der
Wellenfront-Fehler ist 1.27 waves PV und 0.20 waves RMS bei der Bezugswellenlänge
633nm.
Wenn
man als Bezugswellenlänge 550nm annimmt, dann entspricht das 1.46
waves PV und 0.23 waves RMS.
Berechnung
des Korrekturgrads:
spherical
Term, erste Messung: 1.3171
spherical
Term, zweite Messung: 1.2992
spherical
Term, Mittelwert: 1.3081
spherical
Term, theoretischer Wert für Paraboloid: 1.242
Das
ergibt einen Korrekturgrad von 105.3%, also 5.3% überkorrigiert.
3. Ergebnis:
Das auch für mich etwas überraschende Ergebnis dieses Tests ist, dass ein Spiegel beim Foucault-Test so gut abschneiden kann und gleichzeitig beim interferometrischen Test so jämmerlich versagt. Unter diesem Aspekt muss ich meine alten selbstgeschliffenen Spiegel nochmal interferometrisch nachmessen...
Michael
Koch
4. Nachtrag:
Beim Vergleichen mit den Ergebnissen der anderen Teilnehmer ist aufgefallen, dass es signifikante Unterschiede bei der Orientierung der Astigmatismus-Achse gibt. Des Rätsels Lösung besteht darin dass irgend jemand die Markierung am Spiegel geändert haben muss.
Marty
sagt, er hat einen einfachen schwarzen Strich mit Edding gemacht, ohne
auf eine bestimmte Ausrichtung zum Astigmatismus zu achten. Diese Markierung
wurde von den ersten Hälfte der Teilnehmer verwendet, zumindest bis
einschliesslich Horia Costache.
Stathis
Kafalis hat den Spiegel bereits mit neuen Markierungen bekommen, und alle
folgenden Teilnehmer haben diese neuen Markierungen verwendet. Es gibt
zwei neue Markierungen, eine ist mit "1|4" beschriftet, und die andere
um 90 Grad versetzt mit "3" beschriftet, und zusätzlich mit einem
Linsen-Symbol versehen.
Glücklicherweise
sind auf dem Spiegelrand auch noch jede Menge weisse Linien, und auf einem
Foto von Horia Costache kann man sehen wo die ursprüngliche Markierung
relativ zu den weissen Linien gewesen ist. Die weissen Linien sind immer
noch vorhanden, allerdings nicht mehr so deutlich. Aber man kann rekonstruieren
wo die ursprüngliche Markierung gewesen sein muss. Siehe folgendes
Bild, es zeigt die Lage aller weisser Linien und aller Markierungen. An
der Stelle wo die ursprüngliche Markierung gewesen sein muss ist jetzt
absolut NICHTS mehr zu sehen.
Auffällig
ist, dass die neuen Markierungen nahezu perfekt die Achse des Astigmatismus
angeben. Wodurch das Erkennen des Astigmatismus mittels Foucault-Test zusätzlich
erschwert wird. Wer auch immer die ursprüngliche Markierung entfernt
hat, das war ziemlich unfair gegenüber den anderen Teilnehmern.
Der
Winkel zwischen der ursprünglichen Markierung und der neuen "1|4"
Markierung ist ca. 49 Grad.
5. Nachtrag:
Der
Spiegel wurde während der Messungen auf zwei Punkten gelagert, im
Abstand
von 10cm. Dabei hat der Spiegel frei gestanden, die auf die Rückseite
einwirkenden Kräfte waren Null oder sehr klein.
Der
berechnete Teststand-Astigmatismus entspricht 0.11 waves PV in der Wellenfront
(bei 633nm).
Begründung
für den Umrechnungsfaktor 2 siehe unten.
Wenn
man nach Abzug des Teststand-Astigmatismus alle sonstigen Fehler abziehen
würde, dann würde folgender Astigmatismus übrig bleiben:
Zernike
Koeffizient Z4 des Spiegels: (0.4161 - (-0.5273)) / 2 = 0.4717
Zernike
Koeffizient Z5 des Spiegels: (0.0265 - (-0.0303)) / 2 = 0.0284
Betrag
des Astigmatismus des Spiegels: sqrt(0.4717^2 + 0.0284^2) = 0.473
Das
entspricht 2 * 0.473 = 0.945 waves PV in der Wellenfront (bei 633nm).
Bei
550nm entspricht das 1.088 waves PV in der Wellenfront.
Begründung
für den Umrechnungsfaktor 2:
Das
Zernike-Polynom für Astigmatismus ist z[4] = r^2 * cos(2 * winkel),
das Minimum dieser Funktion ist -1 und das Maximum ist +1, daher muss man
mit dem Faktor 2 multiplizieren um von den Zernike-Koeffizienten zum PV
Wert zu kommen.
Dieser
Faktor ist aber nicht für alle Zernike-Koeffizienten gleich 2, es
gibt unterschiedliche Faktoren!
Noch
ein Hinweis zur Nummerierung der Zernike-Koeffizienten. Es gibt in der
Literatur verschiedene Methoden der Durchnummerierung. Zum Beispiel unterscheidet
sich die Nummerierung von IntelliWave von der Nummerierung die ich in meiner
Formelsammlung verwende:
IntelliWave
(verwendet die "University of Arizona Zernikes") : Astigmatismus = Z5,
Z6
Meine
Formelsammlung: Astigmatismus = Z4, Z5
FringeXP,
Seidel: Astigmatismus = Z4, Z5